S hình tam giác: 5 bí quyết vẽ đẹp như tranh vẽ chuyên nghiệp [Bí quyết số 4 sẽ khiến bạn ngạc nhiên]

Hình Tam Giác là một hình học cơ bản và quen thuộc nhất với chúng ta. Nó là một hình đa giác có ba cạnh và ba góc. Khi các đỉnh của Hình Tam Giác nằm trên cùng một đường thẳng, ta gọi đó là Tam Giác Cân. Khi Tam Giác có một góc vuông và hai cạnh vuông góc (cạnh không vuông góc được gọi là cạnh kề cạnh góc vuông), ta gọi đó là Tam Giác Vuông. Khi ba cạnh của Tam Giác đều bằng nhau, ta gọi đó là Tam Giác Đều.

Các yếu tố cần có để tạo thành Hình Tam Giác là ba đường thẳng khác nhau, không thể song song, và không thể chéo nhau.

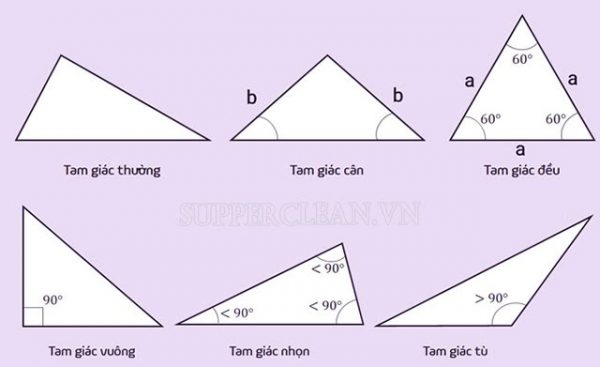
Các loại Hình Tam Giác và đặc điểm của chúng

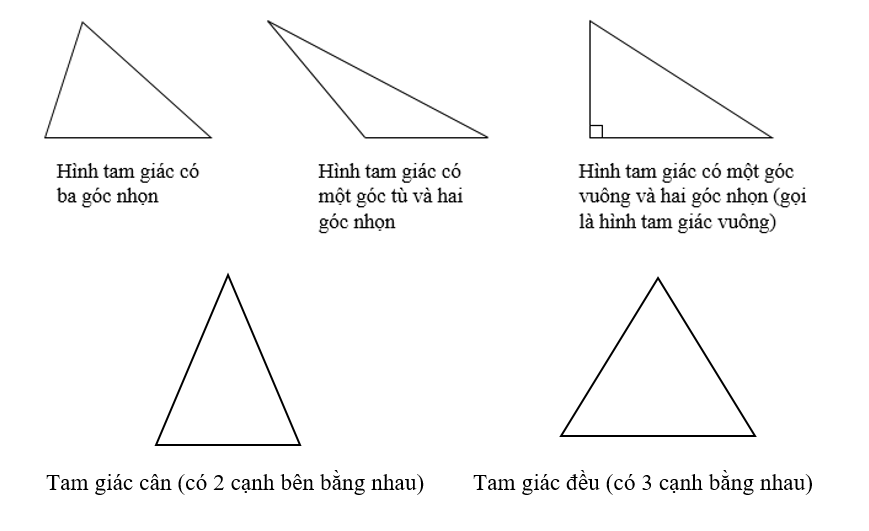
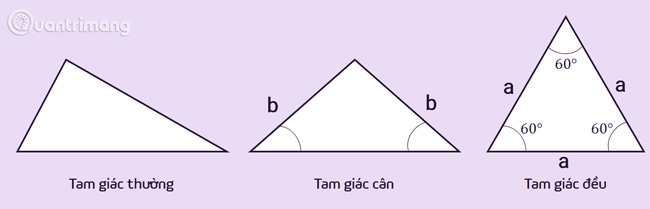
Hình Tam Giác có ba loại chính: Tam giác cân, tam giác vuông và tam giác đều.

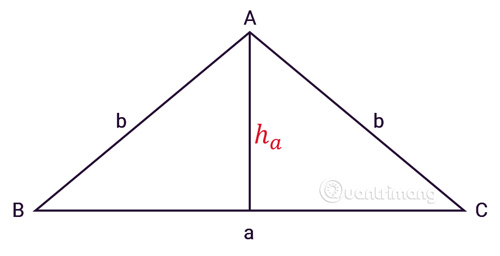
– Tam giác cân: Hai đường cao của tam giác cân bằng nhau và cắt nhau ở trung điểm của đáy của tam giác. Tam giác cân có thể là tam giác vuông hoặc tam giác thường. Tam giác thường là tam giác không có góc bằng nhau và đường cao không cắt đường trung tuyến.
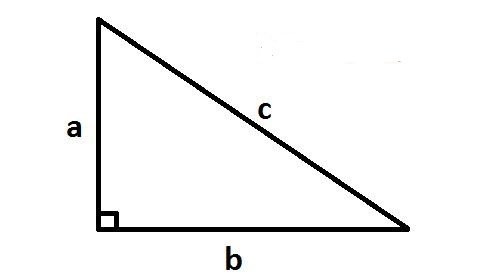
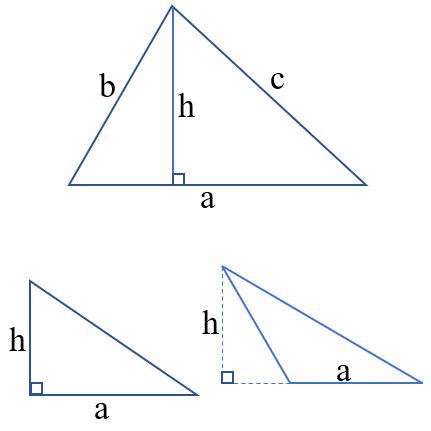
– Tam giác vuông: Tam giác vuông có một góc bằng 90 độ và hai đường góc kề với góc vuông. Đường cao của tam giác vuông là đoạn thẳng nối đỉnh vuông góc tới đáy của tam giác. Ba cạnh của tam giác vuông có thể được sử dụng cho định lý Pythagoreos.
– Tam giác đều: Tam giác đều có ba cạnh bằng nhau và ba góc bằng nhau. Tam giác đều cũng là một loại tam giác cân và tam giác đều.

Công Thức và Tính Chất của Hình Tam Giác

Công thức tính chu vi và diện tích Hình Tam Giác:

– Chu vi tam giác bằng tổng ba cạnh của nó.
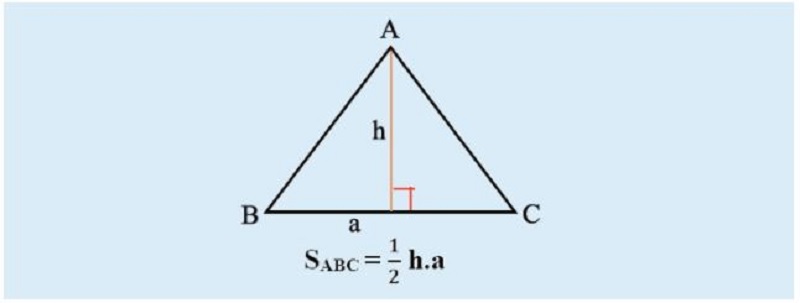
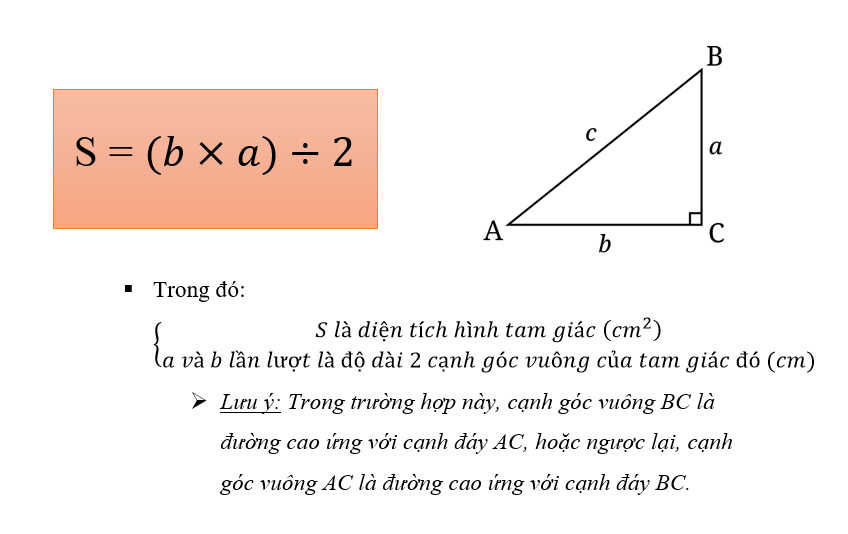
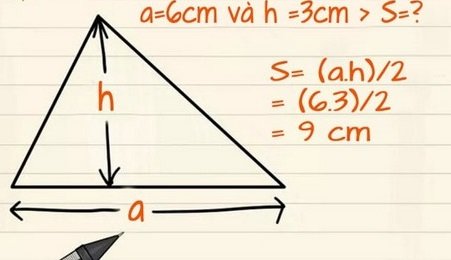
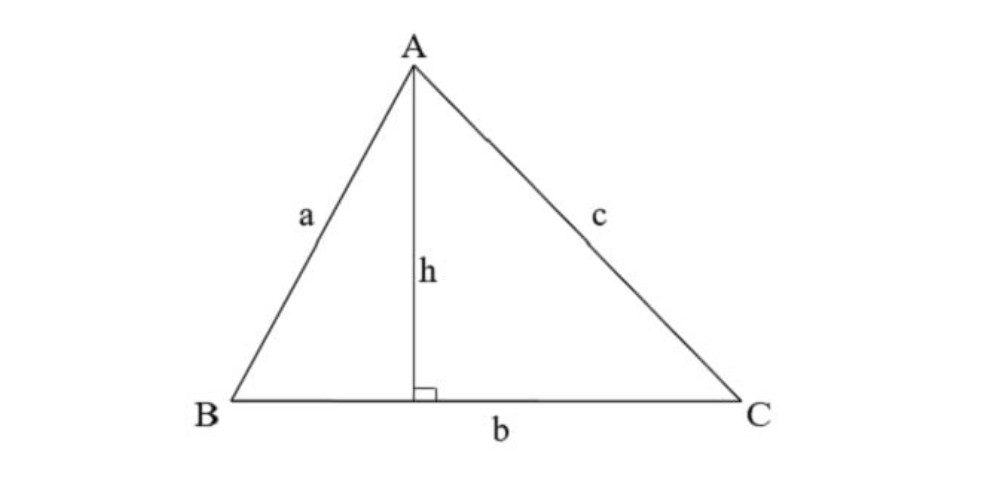
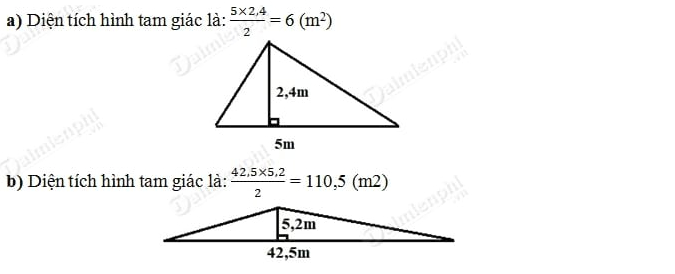
– Diện tích tam giác bằng một nửa tích của cạnh gấp đôi và đường cao tương ứng:

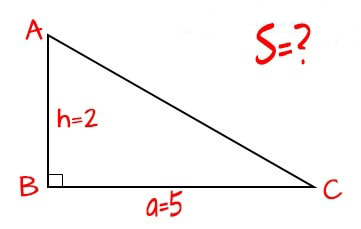
S = 1/2 * a * h

Tính chất của Hình Tam Giác liên quan đến cạnh, đường cao, đường trung tuyến, đường phân giác:

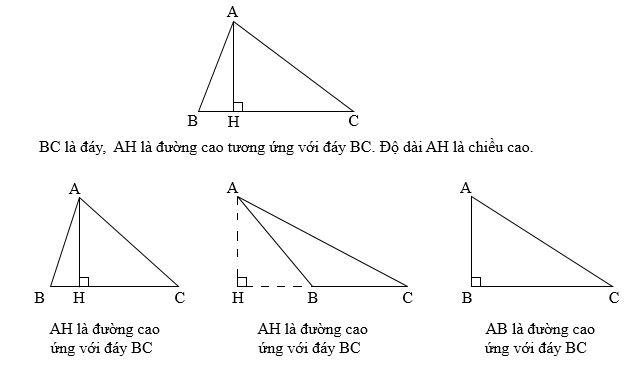
– Đường cao của tam giác là đoạn thẳng kết nối đỉnh và đường thẳng nằm vuông góc với đáy tương ứng.
– Đường trung tuyến của tam giác là đoạn thẳng kết nối trung điểm hai cạnh của tam giác.
– Đường phân giác của tam giác là đoạn thẳng kết nối đỉnh của tam giác với điểm trên đường thẳng đặt tại đáy của tam giác và chia đường thẳng thành hai phần bằng nhau. Đường phân giác cũng chia góc tương ứng thành hai góc bằng nhau.

Ứng Dụng của Hình Tam Giác và Cách Giải Bài Tập liên quan

Các bài toán thực tế liên quan đến Hình Tam Giác và cách giải quyết chúng:

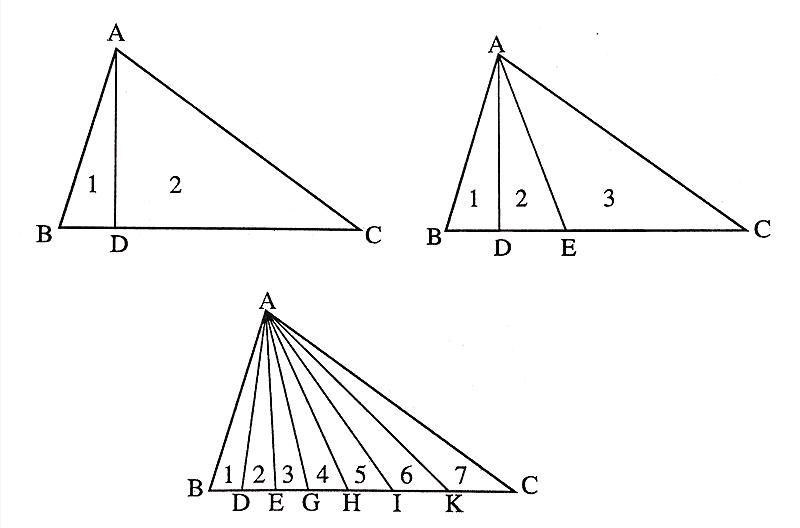
– Tính diện tích đất trống giữa các dãy nhà. Bài toán này yêu cầu tính diện tích tam giác lớn và trừ đi diện tích các tam giác nhỏ hơn.
– Tính tốc độ một chuyển động. Bài toán này yêu cầu tính khoảng cách giữa hai vật trong vị trí khác nhau tại hai thời điểm khác nhau để tính tốc độ chuyển động của một trong hai vật.
– Xác định chiều cao của trụ. Bài toán này yêu cầu tính toán đường cao của tam giác cắt bởi mặt phẳng vuông góc với đáy của trụ.

Cách sử dụng công thức và tính chất để giải các bài tập liên quan đến Hình Tam Giác:

– Sử dụng hệ thức chu vi tam giác để tìm chu vi tam giác bằng cách tính tổng ba cạnh của tam giác.
– Sử dụng công thức tính diện tích tam giác để tìm diện tích tam giác bằng một nửa tích của cạnh gấp đôi và đường cao tương ứng.
– Sử dụng định lý Pythagoreos để tìm bề mặt của tam giác vuông.
– Sử dụng tính chất đường cao, đường trung tuyến và đường phân giác để giải các bài toán có liên quan.

Một Số Định Lý Quan Trọng liên quan đến Hình Tam Giác

– Định lý Pythagoreos: Trong một tam giác vuông, bình phương của độ dài cạnh huyền bằng tổng bình phương của độ dài hai cạnh góc vuông.
– Định lý hình học Euclid: Nếu một đường thẳng chia đôi một tam giác sao cho các đường trung tuyến và đường phân giác của nó giao nhau tại một điểm, thì điểm đó là trung điểm của đường trung tuyến và đường phân giác.
– Định lý ức chế: Trong một tam giác, nếu một cạnh có độ dài lớn hơn số tổng độ dài hai cạnh còn lại, thì tam giác không thể tồn tại.

Phương Pháp Tìm Đường Cao, Đường Trung Tuyến và Đường Phân Giác của Hình Tam Giác

– Cách tìm đường cao của Hình Tam Giác: Sử dụng định nghĩa đường cao để tính độ dài đường cao theo đỉnh và độ dài đáy tương ứng.
– Cách tìm đường trung tuyến của Hình Tam Giác: Sử dụng định nghĩa đường trung tuyến để tính độ dài đường trung tuyến theo độ dài hai cạnh của tam giác.
– Cách tìm đường phân giác của Hình Tam Giác: Sử dụng công thức tính đường phân giác của Hình Tam Giác để tính độ dài đường phân giác theo độ dài hai cạnh của tam giác.