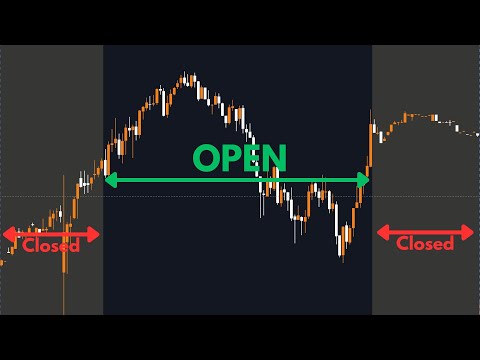
Hoeveel Lichaamsdiagonalen Heeft Een Balk? Een Verhelderend Inzicht!
NỘI DUNG
H1 V1 Som 66 Hoeveel Lichaamsdiagonalen Heeft Een Balk Welke Heeft Pqrs Tuvw Hoeveel Zijvlakken
Keywords searched by users: hoeveel lichaamsdiagonalen heeft een balk hoeveel lichaamsdiagonalen heeft een prisma, lichaamsdiagonaal balk, hoeveel zijvlakken heeft een kubus, hoeveel ribben heeft een balk, hoeveel hoekpunten heeft een balk, lichaamsdiagonaal balk berekenen, eigenschappen kubus, eigenschappen cilinder
Hoeveel lichaamsdiagonalen heeft een balk?
Wat is een lichaamsdiagonaal?
Een lichaamsdiagonaal is een diagonale lijn die door het interieur van een ruimtelijke figuur loopt, van het ene hoekpunt naar het tegenoverliggende hoekpunt. Deze diagonaal snijdt de binnenkant van de figuur en verbindt twee niet-aangrenzende hoekpunten. In het geval van een balk is een lichaamsdiagonaal een diagonale lijn die door het binnenste van de balk loopt, van het ene hoekpunt naar het tegenovergestelde hoekpunt, en die niet samenvallen met een ribbe van de balk.
Definitie van een lichaamsdiagonaal
In een rechthoekige balk, die ook wel een rechthoekig blok wordt genoemd, zijn de zijden vlakken die elkaar loodrecht snijden. De zijvlakken worden ribben genoemd en elke ribbe vormt één zijde van de balk. Een balk heeft in totaal zes ribben, die elk een zijde van de balk vertegenwoordigen.
Daarnaast zijn er ook diagonalen in een balk. Deze diagonalen zijn lijnen die de hoekpunten van de ribben met elkaar verbinden en door het binnenste van de balk lopen. Een lichaamsdiagonaal gaat door het interieur van de balk, terwijl een vlakdiagonaal zich op het oppervlak van de balk bevindt. Een lichaamsdiagonaal moet voldoen aan de voorwaarde dat deze niet samenvalt met een ribbe van de balk.
Hoeveel lichaamsdiagonalen heeft een balk?
Om het aantal lichaamsdiagonalen in een balk te berekenen, kunnen we gebruikmaken van een formule. Het aantal lichaamsdiagonalen in een balk wordt gegeven door de formule:
n = (1/2) x (a^2 + b^2 + c^2 – 3)
waarbij n het aantal lichaamsdiagonalen is en a, b en c de zijden van de balk zijn.
Aangezien een balk drie zijden heeft, kunnen we deze formule toepassen om het aantal lichaamsdiagonalen te berekenen. Laten we aannemen dat de zijden van de balk respectievelijk a, b en c zijn.
Dan is het aantal lichaamsdiagonalen in de balk gelijk aan:
n = (1/2) x (a^2 + b^2 + c^2 – 3)
Laten we als voorbeeld een balk met zijden van 5 cm, 3 cm en 4 cm nemen. Door deze waarden in de formule in te vullen, kunnen we het aantal lichaamsdiagonalen berekenen.
n = (1/2) x (5^2 + 3^2 + 4^2 – 3)
n = (1/2) x (25 + 9 + 16 – 3)
n = (1/2) x (47)
n = 23.5
Daarom heeft een balk met zijden van 5 cm, 3 cm en 4 cm ongeveer 23.5 lichaamsdiagonalen.
Het aantal lichaamsdiagonalen in een balk kan zowel gehele getallen als halve getallen opleveren. Dit komt omdat de zijden van een balk vaak in decimale getallen worden uitgedrukt en de berekening tot een halve waarde kan leiden. In dit geval wordt het aantal lichaamsdiagonalen afgerond naar het dichtstbijzijnde gehele getal.
Hoe bereken je de lengte van een lichaamsdiagonaal in een balk?
Om de lengte van een lichaamsdiagonaal in een balk te berekenen, kunnen we gebruikmaken van de stelling van Pythagoras. Deze stelling stelt dat in een rechthoekige driehoek, het kwadraat van de lengte van de schuine zijde gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden.
Voor een balk met zijden a, b en c, waarbij c de lichaamsdiagonaal is, kunnen we de lengte van de lichaamsdiagonaal berekenen met behulp van de formule:
c = √(a^2 + b^2 + c^2)
Laten we als voorbeeld een balk nemen met zijden van 3 cm, 4 cm en 5 cm. Door deze waarden in de formule in te vullen, kunnen we de lengte van de lichaamsdiagonaal berekenen.
c = √(3^2 + 4^2 + 5^2)
c = √(9 + 16 + 25)
c = √(50)
c ≈ 7.071 cm
Daarom is de lengte van de lichaamsdiagonaal in een balk met zijden van 3 cm, 4 cm en 5 cm ongeveer 7.071 cm.
Wat zijn de eigenschappen van lichaamsdiagonalen in een balk?
Lichaamsdiagonalen in een balk hebben enkele interessante eigenschappen. Ten eerste zijn alle lichaamsdiagonalen in een balk even lang. Dit betekent dat de lengte van elke lichaamsdiagonaal gelijk is aan die van de andere lichaamsdiagonalen.
Daarnaast zijn lichaamsdiagonalen symmetrisch. Elk paar lichaamsdiagonalen in een balk is evenwijdig en snijdt elkaar in het midden van de balk. Dit betekent dat als twee lichaamsdiagonalen elkaar snijden, ze dit doen op gelijke afstanden van de hoekpunten.
Bovendien staan de lichaamsdiagonalen loodrecht op elkaar. Dit betekent dat elke lichaamsdiagonaal loodrecht staat op de vlakken van de balk. Dit creëert een orthogonaal patroon dat bijdraagt aan de structurele stabiliteit van de balk.
Daarnaast hebben lichaamsdiagonalen ook verbindingen met de zijvlakken van de balk. De lichaamsdiagonalen snijden de zijvlakken van de balk in hun midden. Dit betekent dat als je een lichaamsdiagonaal tekent, deze het zijvlak precies in twee gelijke delen verdeelt.
Hoe zien lichaamsdiagonalen eruit in een driedimensionaal perspectief?
Om een visuele representatie te geven van lichaamsdiagonalen in een balk, kunnen we een driedimensionaal perspectief gebruiken. Stel je bijvoorbeeld een rechthoekige balk voor met zijden van 5 cm, 3 cm en 4 cm.
In dit perspectief zou je vier lichaamsdiagonalen kunnen zien die door het binnenste van de balk lopen, van het ene hoekpunt naar het tegenovergestelde hoekpunt. Deze lichaamsdiagonalen creëren een kruisvormige structuur in het binnenste van de balk, waarbij ze elkaar in het midden van de balk doorsnijden.
Met behulp van een driedimensionaal perspectief kunnen we ook de richtingen van de lichaamsdiagonalen visualiseren. Een lichaamsdiagonaal kan bijvoorbeeld verticaal omhoog gaan vanaf een hoekpunt aan de onderkant van de balk naar het tegenovergestelde hoekpunt aan de bovenkant van de balk. Een andere lichaamsdiagonaal kan horizontaal van links naar rechts lopen, terwijl de overige diagonaal diagonaal van voor naar achter loopt.
Het gebruik van een driedimensionaal perspectief helpt bij het begrijpen van de positie en richting van lichaamsdiagonalen in een balk, waardoor we hun eigenschappen beter kunnen visualiseren.
Hoe onderscheiden lichaamsdiagonalen zich van andere diagonalen in een balk?
In een balk zijn er niet alleen lichaamsdiagonalen, maar ook vlakdiagonalen. Het belangrijkste verschil tussen lichaamsdiagonalen en vlakdiagonalen is dat lichaamsdiagonalen door het binnenste van de balk lopen, terwijl vlakdiagonalen zich op het oppervlak van de balk bevinden.
Lichaamsdiagonalen verbinden twee niet-aangrenzende hoekpunten van de balk en snijden de binnenkant van de balk. Deze diagonale lijnen hebben ook de eigenschap dat ze loodrecht staan op de zijvlakken van de balk.
Aan de andere kant verbinden vlakdiagonalen hoekpunten die zich op het oppervlak van de balk bevinden. Deze diagonalen liggen dus op het oppervlak van de balk en snijden de zijvlakken van de balk.
Daarnaast hebben lichaamsdiagonalen een ander aantal in vergelijking met de vlakdiagonalen. Een balk heeft in totaal vier lichaamsdiagonalen, terwijl er namelijk rekening wordt gehouden met elke zijde van de balk. Aan de andere kant heeft een balk zes vlakdiagonalen, waarbij er voor elk zijvlak van de balk een diagonale lijn wordt getrokken.
Over het algemeen onderscheiden lichaamsdiagonalen zich van vlakdiagonalen doordat ze door het binnenste van de balk lopen en niet samenvallen met de zijvlakken van de balk.
Hoe kunnen lichaamsdiagonalen worden gebruikt bij het berekenen van andere eigenschappen van een balk?
Lichaamsdiagonalen kunnen worden gebruikt bij het berekenen van andere eigenschappen van een balk. Een van de toepassingen van lichaamsdiagonalen is bijvoorbeeld het berekenen van de lengte van een ribbe of de diagonaal van een zijvlak van de balk.
Door de lengte van een l
Categories: Update 34 Hoeveel Lichaamsdiagonalen Heeft Een Balk

Een lichaamsdiagonaal gaat door het midden van de balk heen. Een balk heeft 4 lichaamsdiagonalen.Kubus: Elke ribbe kun je verbinden met één andere ribbe om een diagonaalvlak te krijgen, er zijn 12 ribben dus 12/2=6 12 / 2 = 6 diagonaalvlakken. Elk hoekpunt kun je met één ander hoekpunt verbinden door een lichaamsdiagonaal, er zijn 8 hoekpunten dus 8/2=4 8 / 2 = 4 lichaamsdiagonalen.Voor de lengte d van een lichaamsdiagonaal in een balk met ribben van lengte a , b en c geldt: d 2 = a 2 + b 2 + c 2 .
Hoeveel Lichaamsdiagonalen Heeft Een Kubus?
Hoe Bereken Je De Lichaamsdiagonaal Van Een Balk?
Om de lichaamsdiagonaal (d) van een balk te berekenen, moet je de lengte (a), breedte (b) en hoogte (c) van de balk kennen. De formule om de lichaamsdiagonaal te berekenen is d² = a² + b² + c².
Hoeveel Lichaamsdiagonalen?
Hoeveel Lichaamsdiagonalen Heeft Een Vierkant?
Hoe Veel Ribben Heeft Een Balk?
Samenvatting 40 hoeveel lichaamsdiagonalen heeft een balk
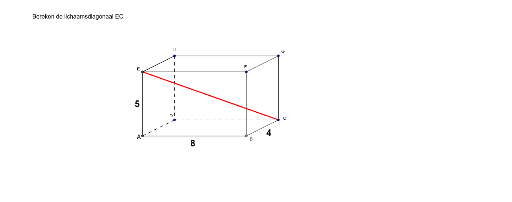
See more here: huanluyenchosaigon125.com
Learn more about the topic hoeveel lichaamsdiagonalen heeft een balk.
- Balken – ribben, diagonalen en lijnen – Slimleren
- Ruimtelijke figuren
- lichaamsdiagonaal – Appspot
- Lichaamsdiagonaal – Wikipedia
- Ruimtelijke figuren – lichaamsdiagonaal
- Balk (meetkunde) – Wikipedia
See more: https://huanluyenchosaigon125.com/videos blog